Rooted Trees
In a rooted tree, one of its vertices is designated as the root. The root provides the tree with an orientation from parent to child. A node with no child is called a leaf. A node that's not a leaf is called an internal node.
 An ordered tree is a rooted tree in which the children of each node are ordered. That is, if a node has children, then there is a first child, a second child, and so on.
An ordered tree is a rooted tree in which the children of each node are ordered. That is, if a node has children, then there is a first child, a second child, and so on.
Representations¶
A rooted tree can be represented in various ways. In this section, we discuss three of them: adjacency list, array-of-parents, and first-child, next-sibling.
The adjacency list representation of a tree \(T\) is an array \(C\) where \(C[v]\) is the children of \(v\), for all nodes in \(T\).
The array-of-parents representation of a tree \(T\) is an array \(P\) where \(P[v]\) is the parent of \(v\) if \(v\) is not the root of T, and P[v] = None otherwise, for all nodes in \(T\).
The first-child next-sibling representation of a tree \(T\) is a pair \((F, N)\) of arrays where:
- \(F[v]\) is the first child of \(v\) if \(v\) is not a leaf node, and
F[v] = Noneotherwise - \(N[v]\) is the next sibiling of \(v\) if \(v\) is not a last child node,
N[v] = Noneotherwise
for all nodes in \(T\).
Based on the context, one or the other of the representations will be best suited. Translating between the representations can be done in linear time.
Examples¶
Let's consider the following rooted tree.
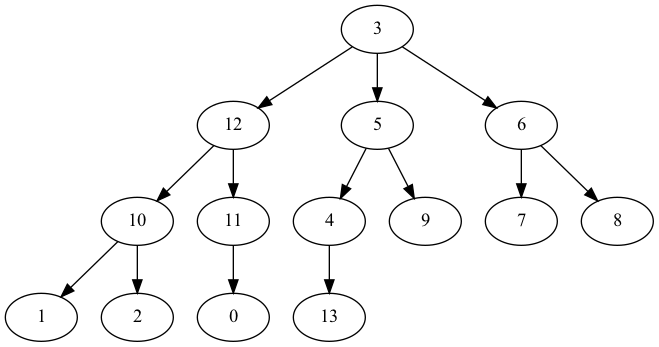
The adjacency list representation of the above tree is
i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
C[i] | [] | [] | [] | [12,5,6] | [13] | [4,9] | [7,8] | [] | [] | [] | [1,2] | [0] | [10,11] | [] |
The array-of-parents representation of the same tree is:
i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
P[i] | 11 | 10 | 10 | None | 5 | 3 | 3 | 6 | 6 | 5 | 12 | 12 | 3 | 4 |
The first-child next-sibiling representation of the same tree is:
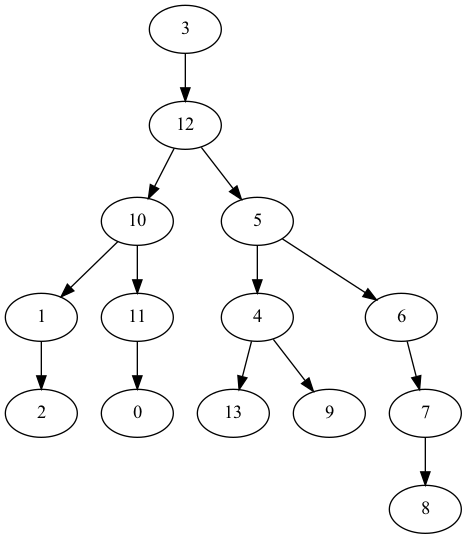
i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
F[i] | None | None | None | 12 | 13 | 4 | 7 | None | None | None | 1 | 0 | 10 | None |
N[i] | None | 2 | None | None | 9 | 6 | None | 8 | None | None | 11 | None | 5 | None |
Free tree to rooted tree¶
def build_graph(n: int, edges: list[tuple[int, int]], root: int):
graph: list[list[int]] = [[] for _ in range(n)]
for a, b in edges:
graph[a].append(b)
graph[b].append(a)
parents: list[Optional[int]] = [None] * n
children: list[list[int]] = [[] for _ in range(n)]
stack = [root]
seen = {root}
while stack:
node = stack.pop()
for child in graph[node]:
if child not in seen:
seen.add(child)
parents[child] = node
children[node].append(child)
stack.append(child)
return parents, children
Let's test it on the following tree:
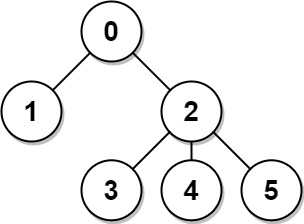
>>> edges = [(0, 1), (0, 2), (2, 3), (2, 4), (2, 5)]
>>> parents, children = build_graph(6, edges, 0)
>>> parents
[None, 0, 0, 2, 2, 2]
>>> children
[[1, 2], [], [3, 4, 5], [], [], []]
Translations between representations¶
From adjacency list to array-of-parents¶
def adjacency_list_to_parents(children_list):
n = len(children_list)
parents = [None] * n
for i, children in enumerate(children_list):
for child in children:
parents[child] = i
return parents
From array-of-parents to adjacency list¶
def parents_to_adjacency_list(parents):
n = len(parents)
children_list = [[] for _ in range(n)]
for i, parent in enumerate(parents):
if parent is not None:
children_list[parent].append(i)
return children_list
Question: Let C be the adjacency list representation of a tree. Let P be the array-of-parents representation of the same tree. Does adjacency_list_to_parents(C) == P always evaluate to True? What about parents_to_adjacency_list(P) == C?
From adjacency list to first-child next-sibling¶
def adjacency_list_to_child_sibling(children_list):
n = len(children_list)
firsts = [None] * n
nexts = [None] * n
for i, children in enumerate(children_list):
prev = None
for j, child in enumerate(children):
if j == 0:
firsts[i] = child
else:
nexts[prev] = child
prev = child
return firsts, nexts
From first-child next-sibling to adjacency list¶
def child_sibling_to_adjacency_list(firsts, nexts):
n = len(firsts)
children_list = [[] for _ in range(n)]
for i, first in enumerate(firsts):
curr = first
while curr is not None:
children_list[i].append(curr)
curr = nexts[curr]
return children_list
TreeNode class¶
Another popular way of representing a rooted tree is pointer-based: each node has an internal list for storing pointers to its children:
class TreeNode:
def __init__(self, id):
self._id = id
self._children = []
@property
def id(self):
return self._id
@property
def children(self):
return self._children
def add_child(self, node):
self._children.append(node)
def is_leaf(self):
return not self._children
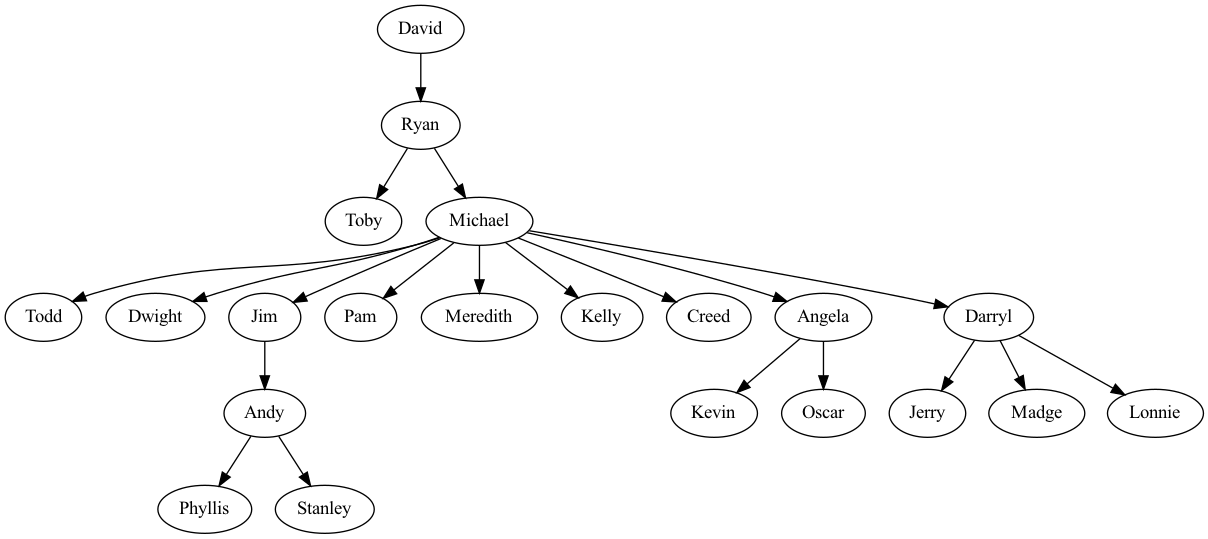
Here's how we construct the office tree shown above:
def construct_the_office_tree_naive():
david = TreeNode("David")
ryan = TreeNode("Ryan")
david.add_child(ryan)
toby = TreeNode("Toby")
ryan.add_child(toby)
michael = TreeNode("Michael")
ryan.add_child(michael)
todd = TreeNode("Todd")
michael.add_child(todd)
dwight = TreeNode("Dwight")
michael.add_child(dwight)
jim = TreeNode("Jim")
michael.add_child(jim)
pam = TreeNode("Pam")
michael.add_child(pam)
meredith = TreeNode("Meredith")
michael.add_child(meredith)
kelly = TreeNode("Kelly")
michael.add_child(kelly)
creed = TreeNode("Creed")
michael.add_child(creed)
angela = TreeNode("Angela")
michael.add_child(angela)
kevin = TreeNode("Kevin")
angela.add_child(kevin)
oscar = TreeNode("Oscar")
angela.add_child(oscar)
andy = TreeNode("Andy")
jim.add_child(andy)
phyllis = TreeNode("Phyllis")
andy.add_child(phyllis)
stanley = TreeNode("Stanley")
andy.add_child(stanley)
darryl = TreeNode("Darryl")
michael.add_child(darryl)
jerry = TreeNode("Jerry")
darryl.add_child(jerry)
madge = TreeNode("Madge")
darryl.add_child(madge)
lonnie = TreeNode("Lonnie")
darryl.add_child(lonnie)
return david
from typing import Iterable
def construct_tree_from_edges(edges: list[tuple[str, str]]) -> TreeNode:
nodes = {}
for parent, child in edges:
if parent not in nodes:
nodes[parent] = TreeNode(parent)
if child not in nodes:
nodes[child] = TreeNode(child)
nodes[parent].add_child(nodes[child])
return find_root(nodes.values())
def find_root(nodes: Iterable[TreeNode]) -> TreeNode:
is_child = set()
for node in nodes:
for child in node.children:
is_child.add(child.id)
for node in nodes:
if node.id not in is_child:
return node
raise ValueError("input is not a valid tree")
Let's see it in action:
>>> edges = [
... ("Ryan", "Toby"),
... ("Ryan", "Michael"),
... ("Michael", "Todd"),
... ("Michael", "Dwight"),
... ("Michael", "Jim"),
... ("Michael", "Pam"),
... ("Michael", "Meredith"),
... ("Michael", "Kelly"),
... ("Michael", "Creed"),
... ("Michael", "Angela"),
... ("Michael", "Darryl"),
... ("Jim", "Andy"),
... ("Andy", "Phyllis"),
... ("Andy", "Stanley"),
... ("Angela", "Kevin"),
... ("Angela", "Oscar"),
... ("Darryl", "Jerry"),
... ("Darryl", "Madge"),
... ("Darryl", "Lonnie"),
... ("David", "Ryan"),
... ]
>>> construct_tree_from_edges(edges).id == "David"
True
The find_root function makes use of the fact that the root node is the only node in a tree that's not a child of anyone else. The implementation above has linear time and space complexity. Can we reduce the space complexity?
Observe that as we traverse the list of nodes, if we put each node and its children into a list, then every node will appear twice, except for the root node which only appears once. Then the unique node can be found using the XOR operator:
from string import ascii_letters
def find_root(nodes: Iterable[TreeNode]) -> TreeNode:
current = 0
for node in nodes:
current ^= _str_to_int(node.id)
for child in node.children:
current ^= _str_to_int(child.id)
for node in nodes:
if _str_to_int(node.id) == current:
return node
def _str_to_int(s: str) -> int:
return sum((ascii_letters.index(char) + 1) * pow(52, i) for i, char in enumerate(s))
Notes:
- This code fragment assumes
node.idonly containsa-zA-Z. string.ascii_lettersis a string of length 52:abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ_str_to_intencodes a string to an integer by base conversion. What happens if one leaves out the+ 1inascii_letters.index(char) + 1)?
Terminology¶
size: The number of vertices in the tree.
The size can be found using a simple recursion:
Iterative DFS:
def get_size_stack(root: TreeNode) -> int:
if root is None:
return 0
stack = [root]
size = 0
while stack:
node = stack.pop()
size += 1
for child in node.children:
stack.append(child)
return size
depth: The number of edges from a given node to the root.
To find the depth of a node, we need to traverse the tree level by level, so BFS is used.
from collections import deque
def get_depth(root: TreeNode, node: TreeNode) -> int:
depth = 0
q = deque([root])
while q:
for _ in range(len(q)):
v = q.popleft()
if v == node:
return depth
for child in v.children:
q.append(child)
depth += 1
raise ValueError("node does not exist in root")
height: The number of edges on the longest path from a given node to a leaf. The height of a tree is the height of its root. Equivalently, the height of a tree is the depth of its deepest leaf. So we can again use BFS.
from collections import deque
def get_height(root: TreeNode) -> int:
depth = 0
q = deque([root])
while q:
for _ in range(len(q)):
v = q.popleft()
for child in v.children:
q.append(child)
depth += 1
return depth - 1
The height of a node \(u\) can also be defined recursively:
- if \(u\) is a leaf, then its height is 0.
- otherwise, its height is one more than the maximum of the heights of its children.
def get_height_recursive(root: TreeNode) -> int:
return max((get_height_recursive(child) for child in root.children), default=-1) + 1
This is a post-order traversal, which is one type of DFS.
siblings: Two nodes that are children of the same parent
from collections import deque
def check_sibling(root: TreeNode, node1: TreeNode, node2: TreeNode) -> bool:
q = deque([root])
while q:
v = q.popleft()
if v in (node1, node2):
return False
if node1 in v.children and node2 in v.children:
return True
for child in v.children:
q.append(child)
return False
ancestor: \(u\) is an ancestor of \(v\) if \(u = v\) or \(u\) is an ancestor of the parent of \(v\).
proper ancestor: A proper ancestor node of \(v\) is an ancestor node of \(v\) that is not \(v\) itself.
descendant: \(u\) is a descendant of \(v\) if \(v\) is an ancestor of \(u\).
proper descendant: A proper descendant node of \(v\) is a descendant node of \(v\) that is not \(v\) itself.
The following code performs an iterative pre-order traversal to search for des in the subtree rooted at anc:
def check_ancestor_iterative(anc: TreeNode, des: TreeNode) -> bool:
stack = [anc]
while stack:
node = stack.pop()
if node == des:
return True
for child in node.children:
stack.append(child)
return False
The code below uses recursion:
def check_ancestor(anc: TreeNode, des: TreeNode) -> bool:
if anc is None:
return False
return anc == des or any(check_ancestor(child, des) for child in anc.children)
Of course, BFS can also be used here. Which traversal is better here, BFS or DFS? Both have linear time complexity, but there is a difference in terms of space complexity. BFS uses O(maxWidth) memory, whereas DFS uses O(height). If the tree is faily full, then O(height) = O(log N) where \(N\) is the size of the tree, and DFS is more space-efficient than BFS.
Lowest Common Ancestor (LCA): The LCA between two nodes \(u\) and \(v\) is the lowest node in the tree that has both \(u\) and \(v\) as descendants.
In the office tree above, Michael is the LCA between Jim and Oscar, Ryan is the LCA between Tobby and Dwight, and Andy is the LCA between Stanley and Andy.
def get_lca(root: TreeNode, u: TreeNode, v: TreeNode) -> TreeNode:
parents = {root.id: None}
stack = [root]
while stack:
node = stack.pop()
for child in node.children:
parents[child.id] = node
stack.append(child)
u_ancestors = set()
u_anc = u
while u_anc is not None:
u_ancestors.add(u_anc.id)
u_anc = parents[u_anc.id]
v_anc = v
while v_anc.id not in u_ancestors:
v_anc = parents[v_anc.id]
return v_anc
Check Two Trees Are Identical¶
Ordered Trees¶
Checking whether two ordered trees are identical can be done recursively:
def same_ordered_tree(tree1, tree2):
return (tree1 is None and tree2 is None) or (
tree1 is not None
and tree2 is not None
and tree1.id == tree2.id
and len(tree1.children) == len(tree2.children)
and all(
same_ordered_tree(c1, c2) for c1, c2 in zip(tree1.children, tree2.children)
)
)
Unordered Trees¶
When the trees are unordered, equalities are checked after sorting children by id. Here we assume the id's are unique.
from operator import attrgetter
def same_unordered_tree(tree1, tree2):
return (tree1 is None and tree2 is None) or (
tree1 is not None
and tree2 is not None
and tree1.id == tree2.id
and len(tree1.children) == len(tree2.children)
and all(
same_unordered_tree(c1, c2)
for c1, c2 in zip(
sorted(tree1.children, key=attrgetter("id")),
sorted(tree2.children, key=attrgetter("id")),
)
)
)
Question: What if the id's are not unique?
Serialization¶
In this section we discuss how to serialize and deserialize a rooted tree.
DFS: Nested Parenthesis Representation¶
def serialize_dfs(root) -> str:
return (
"("
+ str(root.id)
+ "".join(serialize_dfs(child) for child in root.children)
+ ")"
)
Application I: Check Two Unordered Trees Have the Same Structure¶
The following three unordered trees have the same structure:
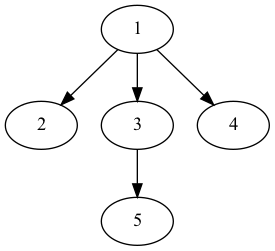
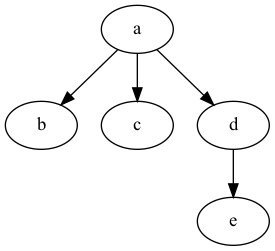
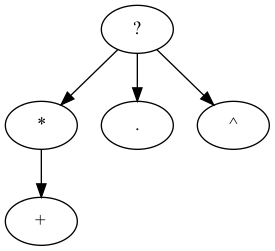
Aho, Hopcroft and Ullman (AHU) algorithm:
def normalize(root: TreeNode) -> str:
children_nums = [normalize(child) for child in root.children]
children_nums.sort()
return "(" + "".join(children_nums) + ")"
The three trees above are normalized to ((())()()).
Application II: Check subtree¶
A subtree of a tree \(T\) is a tree that consists of a node in \(T\) and all of this node's descendants. A tree is considered a subtree of itself.
def is_subtree(tree: TreeNode, subtree: TreeNode) -> bool:
tree_serialized = serialize(tree)
subtree_serialized = serialize(subtree)
return subtree_serialized in tree_serialized
Level-order Traversal¶
Each group of children is separated by a #.
For example, serializing the office tree renders
David,#,Ryan,#,Toby,Michael,#,#,Todd,Dwight,Jim,Pam,Meredith,Kelly,Creed,Angela,Darryl,#,#,#,Andy,#,#,#,#,#,Kevin,Oscar,#,Jerry,Madge,Lonnie,#,Phyllis,Stanley.
from collections import deque
def serialize(root: TreeNode) -> str:
res = []
q = deque([root, None])
while q:
for _ in range(len(q)):
node = q.popleft()
if node is not None:
res.append(node.id)
for child in node.children:
q.append(child)
q.append(None)
else:
res.append("#")
while res and res[-1] == "#":
res.pop()
return ",".join(res)
def deserialize(data: str) -> TreeNode:
if not data:
return None
q = deque()
root = None
for s in data.split(","):
if s == "#":
if len(q) > 1:
q.popleft()
else:
node = TreeNode(s)
if root is None:
root = node
if q:
q[0].children.append(node)
q.append(node)
return root
