Trees and Forests
A forest is an acyclic graph. Any two vertices in a forest are connected by at most one path.
A tree is a connected forest. In other words, all of a forest's components are trees. Any two vertices in a tree are connected by exactly one path.
A forest with \(n\) vertices and \(e\) edges has \(n-e\) components. A tree with \(n\) nodes has \(n-1\) edges. Removing any edge from a tree divides it into two components, and adding any edge creates a cycle.
The leaves of a tree are the nodes with only one neighbor.
Question: Which of the following graphs are trees?
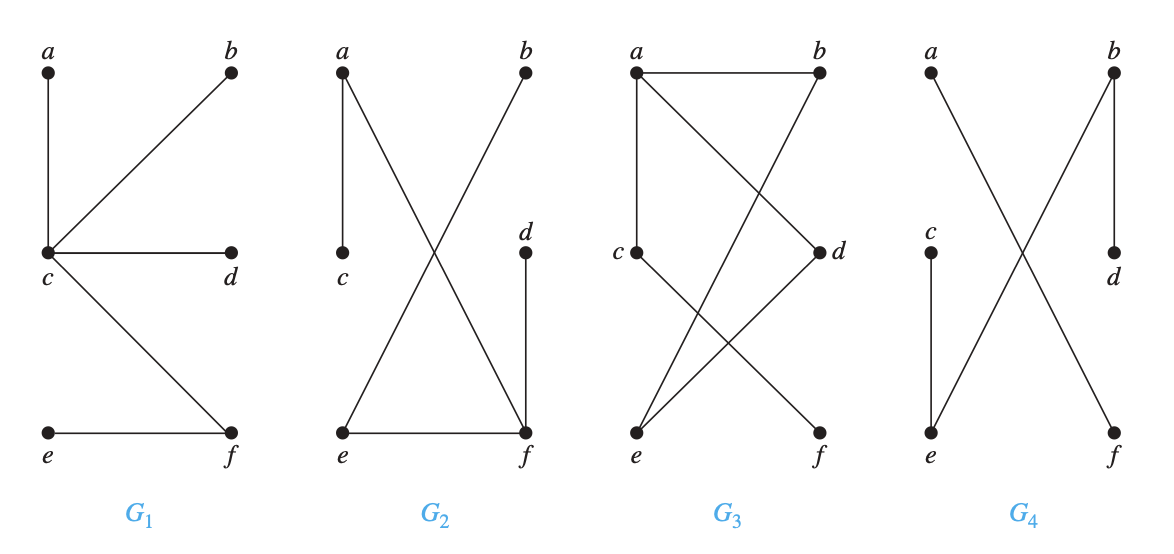
Verify a graph is a forest¶
Given an undirected graph, how do we know if the graph is a forest?
Using DFS, the following function returns True if the input is acyclic.
def is_forest(n: int, edges: list[list[int]]) -> bool:
def has_cycle(root, parent):
if seen[root]:
return False
seen[root] = True
return any(
(seen[nei] and nei != parent) or (not seen[nei] and has_cycle(nei, root))
for nei in graph[root]
)
seen = [False] * n
graph = [[] for _ in range(n)]
for a, b in edges:
graph[a].append(b)
graph[b].append(a)
return not any(has_cycle(i, -1) for i in range(n))
Verify a graph is a tree¶
Given an undirected graph, how do we know if the graph is a tree?
A graph is a tree as long as it satisfies two out of the following three conditions:
- the graph contains \(n - 1\) edges
- the graph does not contain cycles
- the graph is connected
Condition 1 is straightforward to check, as long as we assume that edges are distinct.
The following function checks for conditions 1 and 2.
def is_tree_check_acyclic(n: int, edges: list[list[int]]) -> bool:
return len(edges) == n - 1 and is_forest(n, edges)
The following functions checks for conditions 1 and 3.
def is_tree_check_connected(n: int, edges: list[list[int]]) -> bool:
return len(edges) == n - 1 and _count_components(n, edges) == 1
def _count_components(n: int, edges: list[list[int]]) -> int:
def visit(root):
if not seen[root]:
seen[root] = True
for nei in graph[root]:
visit(nei)
seen = [False] * n
graph = [[] for _ in range(n)]
for a, b in edges:
graph[a].append(b)
graph[b].append(a)
components = 0
for v in range(n):
if not seen[v]:
visit(v)
components += 1
return components
Cayley's Formula¶
Cayley's formula states that there are \(n^{n-2}\) labeled trees on \(n\) nodes. The nodes are labeled \(1, 2, \dots, n\), and two trees are different if either their structures or labelings are different.
For example, when \(n=4\), the number of labeled trees is \(4^{4-2} = 16\):
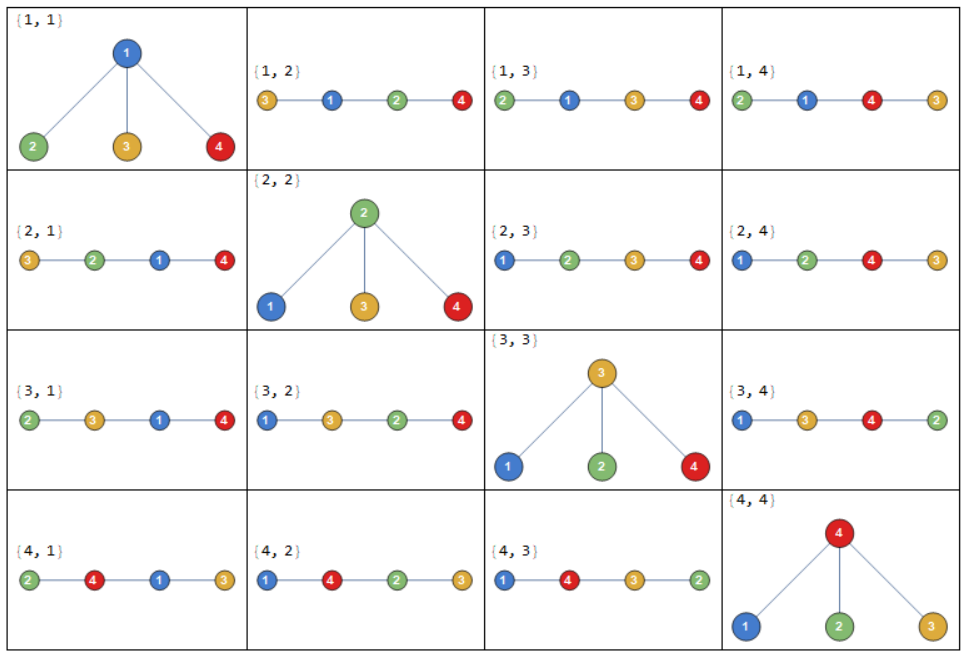
Next we will see how Cayley’s formula can be derived using Prüfer codes.
Prüfer code¶
A Prüfer code is a sequence of \(n − 2\) numbers that describes a labeled tree on \(n\) nodes, and can be generated by a simple iterative algorithm.
Convert a tree into a Prüfer code¶
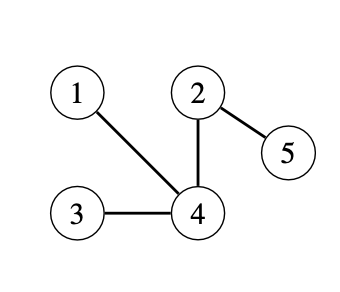
Consider a labeled tree \(T\) with vertices \(\{1, 2, ..., n\}\). At step \(i\), remove the leaf with the smallest label and set the \(i\)th element of the Prüfer sequence to be the label of this leaf's neighbor.
For example, the Prüfer code of the tree below is \([4, 4, 2]\), because we remove leaves \(1\), \(3\), and \(4\).
from heapq import heapify, heappop, heappush
def prufer_code(edges: list[tuple[int, int]]) -> list[int]:
n = len(edges) + 1
graph: list[set[int]] = [set() for _ in range(n + 1)]
for a, b in edges:
graph[a].add(b)
graph[b].add(a)
pc = []
leaves = [vertex for vertex in range(1, n + 1) if len(graph[vertex]) == 1]
heapify(leaves)
for _ in range(n - 2):
leaf = heappop(leaves)
neighbor = graph[leaf].pop()
pc.append(neighbor)
graph[neighbor].remove(leaf)
if len(graph[neighbor]) == 1:
heappush(leaves, neighbor)
return pc
Let's see it in action:
The above implementation runs in \(O(n \log n)\) time.
Observe that each vertex appears in the Prüfer code a fixed number of times - its degree minus \(1\), since the degree will get smaller every time we record its label in the code, and we remove it once the degree is \(1\).
Convert a Prüfer code into a tree¶
Let \({a[0], a[1], ..., a[k-1]}\) be a Prüfer sequence of length \(k\). The tree will have nodes labeled from \(1\) to \(k+2\). For each node set its degree to the number of times it appears in the sequence plus \(1\). Next, for each number in the sequence \(a[i]\), find the first (lowest-numbered) node, \(j\), with degree equal to \(1\), add the edge \((j, a[i])\) to the tree, and decrement the degrees of \(j\) and \(a[i]\). At the end of this loop two nodes with degree \(1\) will remain (call them \(u\) and \(v\)). Lastly, add the edge \((u,v)\) to the tree.
def to_tree(pc: list[int]) -> list[tuple[int, int]]:
n = len(pc) + 2
edges = []
degrees = [1] * (n + 1)
for v in pc:
degrees[v] += 1
leaves = [v for v in range(1, n + 1) if degrees[v] == 1]
for v in pc:
i = heappop(leaves)
edges.append((v, i))
degrees[v] -= 1
if degrees[v] == 1:
heappush(leaves, v)
edges.append((heappop(leaves), heappop(leaves)))
return edges
Relation to Cayley's Formula¶
The immediate consequence is that Prüfer sequences provide a bijection between the set of labeled trees on \(n\) vertices and the set of sequences of length \(n − 2\) on the labels \(1\) to \(n\). The latter set has size \(n^{n−2}\), so the existence of this bijection proves Cayley's formula.
Distance Measures¶
eccentricity: The eccentricity of a vertex \(v\) is the maximum distance between \(v\) and any other vertex in the tree.
The following function uses DFS to find the eccentricity of a vertex in a graph represented as an adjacency list.
def eccentricity_dfs(graph: list[list[int]], vertex: int) -> int:
def dfs(root, parent):
return 1 + max(
(dfs(neighbor, root) for neighbor in graph[root] if neighbor != parent),
default=-1,
)
return dfs(vertex, -1)
Below is the BFS version:
from collections import deque
def eccentricity_bfs(graph: list[list[int]], vertex: int) -> int:
seen = [False] * len(graph)
seen[vertex] = True
dist = 0
q = deque([vertex])
while q:
for _ in range(len(q)):
node = q.popleft()
for child in graph[node]:
if not seen[child]:
seen[child] = True
q.append(child)
dist += 1
return dist - 1
Let's see it in action:
graph = [[1], [0, 2, 3, 5], [1], [1, 4], [3], [1, 6], [5]]
assert eccentricity_bfs(graph, 0) == eccentricity_dfs(graph, 0) == 3
assert eccentricity_bfs(graph, 1) == eccentricity_dfs(graph, 1) == 2
assert eccentricity_bfs(graph, 2) == eccentricity_dfs(graph, 2) == 3
assert eccentricity_bfs(graph, 3) == eccentricity_dfs(graph, 3) == 3
assert eccentricity_bfs(graph, 4) == eccentricity_dfs(graph, 4) == 4
assert eccentricity_bfs(graph, 5) == eccentricity_dfs(graph, 5) == 3
assert eccentricity_bfs(graph, 6) == eccentricity_dfs(graph, 6) == 4
Let's also augment eccentricity_bfs to also include the node that's furthest away from the input:
from collections import deque
def eccentricity(graph: list[list[int]], vertex: int) -> tuple[int, int]:
node = vertex
q = deque([node])
seen = [False] * len(graph)
seen[node] = True
dist = 0
while q:
for _ in range(len(q)):
node = q.popleft()
for child in graph[node]:
if not seen[child]:
seen[child] = True
q.append(child)
dist += 1
return node, dist - 1
diameter: The maximum eccentricity of any vertex in the tree.
peripheral vertex: A vertex of maximum eccentricity.
periphery: The set of peripheral vertices.
To find the diameter of a tree, we first find the farthest node from an arbitrary node a, and name this node b. Then the diameter of the tree is the eccentricity of b.
def get_diameter(tree: list[list[int]]) -> int:
peripheral_node, _ = eccentricity(tree, 0)
_, diameter = eccentricity(tree, peripheral_node)
return diameter
radius: The minimum eccentricity of any vertex in the tree.
A tree's radius \(r\) is related to its diameter \(d\): \(r = \lceil d / 2 \rceil\).
central node: A vertex of minimum eccentricity.
center: The set of central nodes.
Theorem: A tree can have either one or two central nodes. In the case of two central nodes, the two central nodes are adjacent.
centered tree: A tree with only one center.
bicentered tree: A tree with two centers.
def find_center(n: int, edges: list[tuple[int, int]]) -> list[int]:
if n <= 2:
return list(range(n))
graph: list[set[int]] = [set() for _ in range(n)]
for a, b in edges:
graph[a].add(b)
graph[b].add(a)
leaves = [v for v, neighbors in enumerate(graph) if len(neighbors) == 1]
nodes_remaining = n
while nodes_remaining > 2:
new_leaves = []
for leaf in leaves:
nodes_remaining -= 1
neighbor = graph[leaf].pop()
graph[neighbor].remove(leaf)
if len(graph[neighbor]) == 1:
new_leaves.append(neighbor)
leaves = new_leaves
return leaves
